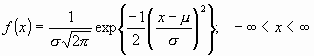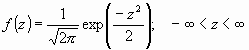lunes, 2 de junio de 2014
La distribución normal
La distribución normal fue reconocida por primera vez por el francés Abraham de Moivre (1667-1754). Posteriormente, Carl Friedrich Gauss (1777-1855) elaboró desarrollos más profundos y formuló la ecuación de la curva; de ahí que también se la conozca, más comúnmente, como la "campana de Gauss". La distribución de una variable normal está completamente determinada por dos parámetros, su media y su desviación estándar, denotadas generalmente pory
. Con esta notación, la densidad de la normal viene dada por la ecuación:
que determina la curva en forma de campana que tan bien conocemos (Figura 2). Así, se dice que una característicasigue una distribución normal de media
y varianza
, y se denota como
, si su función de densidad viene dada por la Ecuación 1.
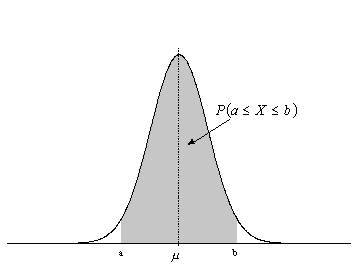
Al igual que ocurría con un histograma, en el que el área de cada rectángulo es proporcional al número de datos en el rango de valores correspondiente si, tal y como se muestra en la Figura 2, en el eje horizontal se levantan perpendiculares en dos puntos a y b, el área bajo la curva delimitada por esas líneas indica la probabilidad de que la variable de interés, X, tome un valor cualquiera en ese intervalo. Puesto que la curva alcanza su mayor altura en torno a la media, mientras que sus "ramas" se extienden asintóticamente hacia los ejes, cuando una variable siga una distribución normal, será mucho más probable observar un dato cercano al valor medio que uno que se encuentre muy alejado de éste.
Propiedades de la distribución normal:La distribución normal posee ciertas propiedades importantes que conviene destacar:
y
es teóricamente posible. El área total bajo la curva es, por tanto, igual a 1.
. Según esto, para este tipo de variables existe una probabilidad de un 50% de observar un dato mayor que la media, y un 50% de observar un dato menor.
). Cuanto mayor sea
, más aplanada será la curva de la densidad.
.
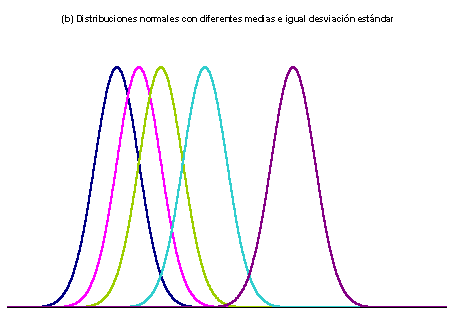
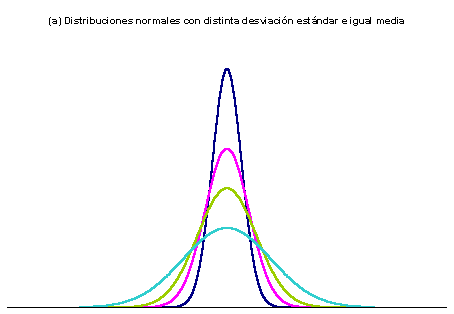
y
(Figura 3). La media indica la posición de la campana, de modo que para diferentes valores de
la gráfica es desplazada a lo largo del eje horizontal. Por otra parte, la desviación estándar determina el grado de apuntamiento de la curva. Cuanto mayor sea el valor de
, más se dispersarán los datos en torno a la media y la curva será más plana. Un valor pequeño de este parámetro indica, por tanto, una gran probabilidad de obtener datos cercanos al valor medio de la distribución.
Como se deduce de este último apartado, no existe una única distribución normal, sino una familia de distribuciones con una forma común, diferenciadas por los valores de su media y su varianza. De entre todas ellas, la más utilizada es la distribución normal estándar, que corresponde a una distribución de media 0 y varianza 1. Así, la expresión que define su densidad se puede obtener de la Ecuación 1, resultando:
Es importante conocer que, a partir de cualquier variable X que siga una distribución, se puede obtener otra característica Z con una distribución normal estándar, sin más que efectuar la transformación:
existen tablas publicadas (Tabla 1) a partir de las que se puede obtener de modo sencillo la probabilidad de observar un dato menor o igual a un cierto valor z, y que permitirán resolver preguntas de probabilidad acerca del comportamiento de variables de las que se sabe o se asume que siguen una distribución aproximadamente normal.
 |
| Figura 3. Ejemplos de distribuciones normales con diferentes parámetros. |
 |
| Tabla 1. Áreas bajo la curva normal estándar. Los valores de la tabla que no se muestran en negrita representan la probabilidad de observar un valor menor o igual a z. La cifra entera y el primer decimal de z se buscan en la primera columna, y el segundo decimal en la cabecera de la tabla. |
Modelos de distribución de probabilidad de variables continua
Al igual que en el caso de las distribuciones de probabilidad de variables discretas, en el caso de las distribuciones de
probabilidad de variables continuas se tienen varios modelos teóricos.
probabilidad de variables continuas se tienen varios modelos teóricos.
- Uniforme. Es la distribución en donde todos los eventos tienen la misma probabilidad.
- Exponencial. Se utiliza para estudiar el tiempo entre dos sucesos.
- Beta. Sirve para el estudio de variaciones, a través de varias muestras, de un porcentaje que representa algún fenómeno.
- Gamma. Se utiliza para estudiar variables cuya distribución puede ser asimétrica.
- ji cuadrada (x^2). Es una distribución asociada a la prueba c², y se usa para comparar los valores observados con los esperados.
- Normal. Es la distribución más utilizada porque la mayoría de las variables utilizadas en fenómenos sociales se distribuyen aproximadamente siguiendo este modelo. Es la que tocaremos a continuación y se le llama comúnmente distribución normal.
Ejemplos de Distribución de probabilidad para variables continuas
- Según estadísticas la probabilidad de que el motor de un auto nuevo, de cierto modelo, y marca sufra de algún desperfecto en los primeros 12 meses de uso es de 0.02, si se prueban tres automóviles de esta marca y modelo, encuentre el número esperado de autos que no sufren de algún desperfecto en los primeros doce meses de uso y su desviación estándar.
Solución:
Haciendo uso de un diagrama de árbol, usando las literales siguientes, se obtiene el espacio muestral d como se muestra a continuación;
N = no sufre de algún desperfecto en el motor los primeros 12 meses de uso
S = sufre de algún desperfecto en el motor los primeros 12 meses de uso
N |
N
S
N
N 
S
S
N
1er auto N
S
S 
N
2o auto S
3o S
d = {NNN, NNS, NSN, NSS, SNN, SNS, SSN, SSS}
x = variable que nos define el número de autos que no sufre de algún desperfecto en el motor durante los primeros 12 meses de uso
x = 0, 1, 2 o 3 autos que no sufren algún desperfecto en el motor en los primeros 12 meses de uso
p(x=0)=p(SSS)=(0.02)(0.02)(0.02)=0.000008
p(x=1)=p(NSS, SNS, SSN)=(0.98)(0.02)(0.02)+(0.02)(0.98)(0.02)+(0.02)(0.02)(0.98)=
=0.001176
p(x=2)=p(NNS,NSN,SNN)=(0.98)(0.98)(0.02)+(0.98)(0.02)(0.98)+(0.02)(0.98)(0.98)==0.057624
p(NNN) = (0.98)(0.98)(0.98) =0.941192
Por tanto la media o valor esperado se determina de la siguiente manera:
m =E(x) = 
(0)(0.000008)+(1)(0.001176)+(2)(0.057624)+(3)(0.941192)=
(0)(0.000008)+(1)(0.001176)+(2)(0.057624)+(3)(0.941192)=
=0.0+0.001176+0.115248+2.823576=2.94@ 3 autos que no sufren algún desperfecto en el motor en los primeros 12 meses de uso
La interpretación de la media o valor esperado es; se espera que los 3 autos probados no sufran de algún desperfecto en el motor en los primeros 12 meses de uso.
s=
= 
=
=
±0.2497@±0.0 autos que no sufren algún desperfecto en su motor en los primeros 12 meses de uso.
±0.2497@±0.0 autos que no sufren algún desperfecto en su motor en los primeros 12 meses de uso.
Interpretación:
En este experimento se espera que los 3 autos probados no sufran de algún desperfecto en su motor en los primeros 12 meses de uso y la variabilidad de este experimento es de cero.
Nota:
La media y la desviación estándar se redondean a un valor entero ya que son la media y desviación de una distribución de probabilidad discreta.
- Se ha detectado en una línea de producción que 1 de cada 10 artículos fabricados es defectuoso; se toman de esa línea tres artículos uno tras otro, a) obtenga la distribución de probabilidad del experimento, b) encuentre el número esperado de artículos defectuosos en esa muestra y su desviación estándar.
Solución:
También haciendo uso de in diagrama de árbol, se obtiene el espacio muestral d
a)
D = objeto defectuoso
N = objeto no defectuoso
d={DDD, DDN, DND, DNN, NDD, NDN, NND, NNN}
Este espacio muestral ha sido obtenido haciendo uso de un diagrama de árbol,
x = Variable que nos define el número de objetos defectuosos encontrados
x = 0, 1, 2 o 3 objetos defectuosos
p(x=0)=p(NNN)=(0.9)(0.9(0.9)=0.729
p(x=1)=p(DNN, NDN, NND)=(0.1)(0.9)(0.9)+(0.9)(0.1)(0.9)+(0.9)(0.9)(0.1)=0.243
p(x=2)=p(DDN, DND, NDD)=(0.1)(0.1)(0.9)+(0.1)(0.9)(0.1)+(0.9)(0.1)(0.1)=0.027
p(x=3)=p(DDD)=(0.1)(0.1)(0.1)=0.001
Distribución de probabilidad
x
|
0
|
1
|
2
|
3
|
P(x)
|
0.729
|
0.243
|
0.027
|
0.001
|
b) 
(0)(0.729)+(1)(0.243)+(2)(0.027)+(3)(0.001)=
(0)(0.729)+(1)(0.243)+(2)(0.027)+(3)(0.001)=
= 0.0 + 0.243 + 0.054 + 0.003 = 0.3 @0 productos defectuosos
Interpretación:
Se espera que ninguno de los productos inspeccionados sea defectuoso.
=± 0.6 =± 1 producto defectuoso
Interpretación:
En este experimento se espera que ninguno de los productos inspeccionados sea defectuoso, pero los resultados de este experimento pueden variar en ± 1 producto defectuoso, por lo que al inspeccionar los 3 productos el numero de productos defectuosos puede variar desde –1 producto defectuoso, hasta 1 producto defectuoso, pero, ¿es posible obtener –1 producto defectuoso?, claro que esto no puede ocurrir, luego el número de productos defectuosos en el experimento variará de 0 a 1 producto defectuoso solamente.
- Según estadísticas, la probabilidad de que un pozo petrolero que se perfore en cierta región pueda ser beneficiado es de 0.30. Se perforan tres pozos en esa región, encuentre el número esperado de pozos que pueden ser beneficiados y su desviación estándar.
Solución:
Se obtiene el espacio muestral d, de la misma forma que se ha hecho en los ejemplos anteriores;
B = se puede el pozo que se perfora
N = no se puede beneficiar el pozo que se perfora
d= {BBB, BBN, BNB, BNN, NBB, NBN, NNB, NNN}
x = variable que nos define el número de pozos que se pueden beneficiar
x = 0, 1, 2 o 3 pozos que se pueden beneficiar
p’(x = 0) = p(NNN) = (0.7)(0.7)(0.7)= 0.343
p(x = 1) = p(BNN, NBN, NNB) = (0.3)(0.7)(0.7)(3)=0.441
p(x = 2) = p(BBN, BNB, NBB) = (0.3)(0.3)(0.7)(3)=0.189
p(x = 3) = p(BBB) =(0.3)(0.3)(0.3)= 0.027
@1 pozo beneficiado
Interpretación:
Se espera que solo 1 de los tres pozos perforados sea el que pueda ser beneficiado.
Suscribirse a:
Entradas (Atom)